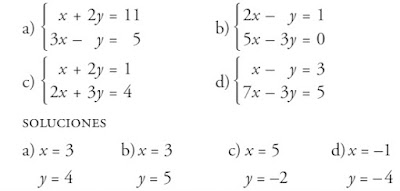CLASE 7: Resolución de problemas con sistemas de ecuaciones.

Buenos días a tod@s!

Vamos a comenzar una nueva semana,  y proseguimos con nuestras clases de Matemáticas on-blog. Espero que os estéis organizando bien casa,  aprovechando el tiempo del mejor modo. La clase de hoy la vamos a dedicar básicamente a resolver problemas, planteando sistemas de ecuaciones. Dedicaremos un par de sesiones a la resolución de problemas antes de explicar el método gráfico.

PROBLEMAS

Realizar en el cuaderno los problemas del  9 al 14 de la página 171 de vuestro libro de Matemáticas.

Recordad que en cada problema debéis seguir una serie de pasos, y tenéis que escribirlos con detalle en vuestro cuaderno. Son los siguientes:

• Indicar a qué se llama x e y.
• Plantear un sistema de ecuaciones con dos incógnitas.
• Resolver el problema, indicando el método empleado (sustitución o reducción)
• Determinar los valores de x e y,  recuadrando las soluciones.
• Comprobar la validez de las soluciones obtenidas. 

Como siempre, una vez realizada la tarea en el cuaderno debéis enviarla escaneada a la dirección de correo:   fedematesxxi@gmail.com

  Este correo también lo tenéis disponible para dudas. Gracias por la atención. 

--------------------------    FIN   DE  LA   CLASE  --------------------------------

Próxima sesión: Miércoles 1  de Abril de 2020

CLASE 6: Resolución de problemas

Buenos días!

Hoy vamos a repasar lo explicado en las dos últimas  clases. Los métodos de sustitución y reducción son dos métodos fundamentales que se usan con frecuencia para resolver infinidad de problemas.
Recordad que cuando estéis haciendo los ejercicios, debéis ir escribiendo todos los pasos en vuestro cuaderno. No sirve de nada dar las soluciones de un sistema, si no indicamos detalladamente todo el proceso seguido. 

La clase de hoy tiene dos partes. En la primera os propongo un ejercicio para que practiquéis la resolución de sistemas usando los métodos estudiados.

En la segunda parte veremos como aplicar estos métodos a la resolución de problemas.

PARTE I:   Realizar en el cuaderno el ejercicio 6 de la página 170 del libro de Matemáticas.

Procurad resolver tres apartados aplicando el método de reducción y otros tres el método de sustitución, comprobando el resultado.

PARTE II: Resolución de problemas.

A continuación os voy a mostrar tres problemas, que se pueden resolver utilizando sistemas de ecuaciones. Copiadlos como ejemplos en vuestro cuaderno, para ir comprendiendo todos los pasos:

Problema 1:   Encuentra dos números cuya suma sea 15 y  el doble del primero menos el triple segundo sea  -5. 

Solución:  Vamos a llamar x e y dichos números. Las ecuaciones planteadas son:

                       x + y = 15

                     2x -  3y =  - 5 

Como la primera ecuación es bastante sencilla, la escogemos para despejar la y. 

Aplicaremos, por tanto el método de sustitución:   y= 15-x

Sustituyendo en la segunda ecuación,  tendremos:    2x - 3(15-x) = - 5 

                                               Quitando paréntesis:   2x - 45 + 3x = - 5

                                        Transponiendo términos:    2x + 3x = + 45 - 5 

                                             Reduciendo términos:            5x = 40

                                                              Despejando.         x= 40/5 = 8

                                                    Solución para x.               x = 8 

Finalmente calculamos el valor de y de la expresión:  y = 15 - x = 15 - 8 = 7.
Los números buscados son:    x=8,  y=7,  como se puede comprobar por sustitución directa.

Problema 2:  En un corral tenemos conejos y gallinas. Hemos contado un total de 25 cabezas, y 70 patas. ¿Cuántos animales hay de cada clase?

Solución:  Vamos a llamar 

x:  número total de conejos  

y:  número total de gallinas.

Como tenemos 25 cabezas, significa que en total hay 25 animales. Luego la primera ecuación es 

x+y=25

Como cada conejo tiene 4 patas y cada gallina 2, la segunda ecuación es:   4x+2y=70

 El sistema que se plantea es: 

                                                  x + y = 25

                                                4x +  2y =  70 

Aplicaremos nuevamente   el método de sustitución, despejando y de la primera ecuación: 

   y= 25-x

Sustituyendo en la segunda ecuación,  tendremos:     4x  + 2(25-x) = 70 

                                               Quitando paréntesis:     4x  + 50 - 2x  = 70 

                                        Transponiendo términos:     4x - 2x = 70 - 50 

                                             Reduciendo términos:            2x = 20

                                                              Despejando.         x= 20/2 =10 

                                                    Solución para x.               x = 10 conejos.

Finalmente calculamos el valor de y de la expresión:  y = 25 - x = 25 - 10  = 15 gallinas.

Deben haber     x = 10 conejos,   y = 15 gallinas.

Problema 3:  En una cafetería hemos tomado dos cafés y tres cruasans, y nos han cobrado 4,60€.

Otro día, por 5 cafés y dos cruasans, nos cobraron 7,10€. ¿Cuál es el precio de un café ? ¿Y de un cruasan?

Solución:  Vamos a llamar 

x:  precio de un café (€)   

y:  precio de un cruasan (€)

Del enunciado del problema podemos deducir el sistema:

                                                   2x + 3y = 4,60

                                                  5x +  2y =  7,10

En este caso, vemos más apropiado aplicar el método de reducción. Para ello multiplicamos la primera ecuación toda por 5 y la segunda por (-2) con el fin de reducir la incógnita x: 

En efecto, 

2x + 3y= 4,60   -->    10 x + 15 y = 23,00

   5x + 2y= 7,10   -->   -10 x - 4 y  = - 14,20  

_________________________________________

    Sumando en columna, obtenemos:   0x + 11 y = 8,80                   

Es decir.   11y = 8,80  -->  y= 8,80 / 11 = 0,80€

Sustituyendo en cualquiera  de las ecuaciones iniciales planteadas, podemos calcular x, Por ejemplo, si tomamos la primera ecuación escribiremos:   2x + 3 ·(0,80) = 4,60
                                                                         2x + 2,40 = 4,60
                                                                         2x = 4,60 - 2,40
                                                                         2x = 2,20 -->  x = 1,10€

En definitiva el precio un café es x= 1,10€  y el de un cruasan   es  y=0,80€

Si has conseguido entender estos problemas, pasamos a la tarea.

TAREA 2:  Realizar en el cuaderno los problemas 1 y 2 de la página 166, usando el método que consideres más adecuado en cada caso.

Como siempre, una vez realizada la tarea en el cuaderno debéis enviarla escaneada a la dirección de correo:   fedematesxxi@gmail.com

  Este correo también lo tenéis disponible para dudas. Gracias por la atención. 

--------------------------    FIN   DE  LA   CLASE  --------------------------------

Próxima sesión: Lunes 30 de Marzo de 2020

CLASE 5: Método de sustitución y reducción

Buenos días!

Hoy vamos a repasar lo explicado en la última  clase y aprender un nuevo método de resolución de ecuaciones: el método de reducción.   Ya sabéis que debéis ir  elaborando vuestros apuntes en el cuaderno de Matemáticas,  copiando algunas de las explicaciones  y luego realizando las tareas propuestas. Así que prestad atención a la pizarra porque comenzamos...

MÉTODO DE SUSTITUCIÓN (Repaso)
Vamos a practicar un poco más el método de sustitución explicado en la última sesión. Recordad que en este método debéis despejar una incógnita de una de las ecuaciones y sustituir en la otra, con el fin de obtener una ecuación de primer grado,  con una sola incógnita. Podéis escoger la ecuación que queráis, pero lo lógico es escoger la ecuación donde la variable a despejar sea más sencilla.

Por ejemplo, si tenemos el sistema:     2x + 5y =12
                                                              4x + y  = 6,

lo más sencillo es despejar y de la segunda ecuación. En ese caso tendríamos y = 6 - 4x.
De ahí sustituimos en la primera, para obtener
                                                              2x + 5 · (6 - 4x) = 12
                                                              2x + 30 - 20x = 12
                                                               2x - 20x = 12 - 30
                                                                  -18x = -18
                                                                        x= +1

Una vez calculado el valor de x, sustituimos en la expresión en negrita, para obtener:

y= 6  - 4 · (+1) =  6 - 4 = 2.

Las soluciones del sistema, son:   x=1,   y=2.

Ahora os toca a vosotros. Debéis hacer en el cuaderno la siguiente tarea:

TAREA 1:

 * Este ejercicio se encuentra en la  página 170 del libro de Matemáticas.
   (No olvides expresar correctamente y por orden los valores de x e y.)


MÉTODO DE REDUCCIÓN.
El método de reducción consiste en multiplicar las dos ecuaciones del sistema por números adecuados, con el fin de, al sumar las expresiones obtenidas, eliminar una de las incógnitas.

Veamos algunos ejemplos sencillos.


Ejemplo 1: Resuelve por reducción el sistema     2x + 3y= 8
                                                                               3x - 5y = -7 

Si por ejemplo queremos eliminar (reducir) la incógnita x, lo que hacemos es fijarnos en sus coeficientes. El truco está en multiplicar la primera ecuación por 3 (coeficiente de la segunda) y la segunda por (-2), que es el coeficiente de la primera, pero cambiado de signo!
De este modo podremos escribir.

              2x + 3y = 8  --> (por 3)    -->   6x + 9y = 24
              3x  - 5y = -7 --> (por -2)  -->  -6x +10y = +14 

Al sumar ambas expresiones en columna, vemos que las x se van ( 6x - 6x = 0)
los coeficientes en y se suman, obteniendo 9y + 10y = 19y   y los términos independientes también se suman  obteniendo  24 + 14 = 38.
Es decir al sumar en columna las dos ecuaciones se reducen a 0x + 19y= 38, es decir
19y= 38, y por tanto  y=38/19 = 2.

Una vez obtenida el valor de la y, podemos sustituir en cualquiera de las ecuaciones iniciales dadas, para determinar el valor de x. Así, si cogemos por ejemplo la primera ecuación, escribiremos:

                   2x  + 3·2 = 8 -->  2x + 6 = 8  --> 2x =8-6 = 2  --> 2x=2  --> x = 1

La solución del sistema es el par ordenado  x=1, y=2.   


Ejemplo 2: Resuelve por reducción el sistema     3x - 2y= 7
                                                                               5x - 3y = 12 

Si por ejemplo queremos eliminar (reducir) la incógnita x, como antes, lo que hacemos es.

• Multiplicar la primera ecuación toda por 5.
• Multiplicar la segunda ecuación toda por (-3)
• Fijaos que son los coeficientes de la x, intercambiados.

 De este modo podremos escribir.

              3x - 2y = 7     --> (por 5)    -->   15x - 10y = 35
              5x  - 3y = 12  --> (por -3)   -->  -15x + 9y = -36

Al sumar ambas expresiones en columna, vemos que las x se van ( 15x - 15x = 0)
los coeficientes en y se suman, obteniendo -10y + 9y = - y   y los términos independientes también se restan  obteniendo  35  - 36  = -1
Es decir al sumar en columna las dos ecuaciones se reducen a 0x -  y= -1 , es decir  y=1.

Una vez obtenida el valor de la y, podemos sustituir en cualquiera de las ecuaciones iniciales dadas, para determinar el valor de x. Así, si cogemos por ejemplo la primera ecuación, escribiremos:

                   3x  - 2 · 1  = 7 -->  3x - 2  = 7 --> 3x =7 + 2  = 9  --> 3x=9  --> x = 9/3 = 3

La solución del sistema es el par ordenado  x=3, y=1.   


Como podéis comprobar al principio parece algo lioso, pero si lo leeis despacio, veréis que solo es multiplicar y sumar o restar, para obtener una ecuación reducida, muy fácil de resolver.

Una vez tengáis copiados estos ejemplos en vuestro cuaderno,  vamos a practicar un poco, hasta comprenderlo bien:


TAREA 2:   Realizar los ejercicios 5, 6 y 7 de la página 165, sobre resolución de sistemas por el método de reducción, detallando el proceso seguido.

Podéis consultar las soluciones de este último ejercicio  en vuestro libro de Matemáticas 2ºESO.

Como siempre, una vez realizada la tarea en el cuaderno debéis enviarla escaneada a la dirección de correo:   fedematesxxi@gmail.com

  Este correo también lo tenéis disponible para dudas. Gracias por la atención. 

--------------------------    FIN   DE  LA   CLASE  --------------------------------

Próxima sesión: Viernes 27 de Marzo de 2020

Clase 4: Sistemas de ecuaciones

Buenos días!

Hoy lunes, vamos a comenzar un tema nuevo, pero que es continuación del tema de ecuaciones. Se trata del tema 8 del libro y tiene por título "Sistemas de ecuaciones".  Ya sabéis que debéis ir  elaborando vuestros apuntes en el cuaderno de Matemáticas,  copiando algunas de las explicaciones  y luego realizando las tareas propuestas. Así que prestad atención a la pizarra porque comenzamos...

¿QUÉ VAMOS A APRENDER EN ESTE TEMA?

En este tema (tema 8 del libro), vamos a ver un tipo de ecuaciones muy particular.

Un sistema de ecuaciones lineales es un conjunto de ecuaciones con varias incógnitas. Como esto puede ser muy complicado, nosotros sólo vamos a aprender a reconocer y resolver sistemas de dos ecuaciones con dos incógnitas, aunque ya os adelanto que hay sistemas de tres ecuaciones con tres incógnitas e incluso de veinte ecuaciones con veinte incógnitas (eso se lo dejamos a los de Bachillerato)

Lo que vamos aprender:

• Reconocer un sistema de ecuaciones lineales.
• Resolver sistemas de ecuaciones por el método de sustitución.
• Resolver sistemas de ecuaciones por el método de reducción.
• Resolver problemas de ecuaciones con algunos de los métodos estudiados.
• Resolver sistemas de ecuaciones por el método gráfico.

¿QUÉ ES UN SISTEMA DE ECUACIONES LINEALES?
 Un sistema de dos ecuaciones lineales con dos incógnitas (x,y), es un conjunto formado por dos ecuaciones del tipo: ax + by =c.

Ejemplos:   Son sistemas de este tipo:

Fijaos la forma que tienen. Sólo aparece la x y la y, acompañado de unos coeficientes e igualado a un número. Cuando algunas de las incógnitas aparece elevada a dos, o tres ya no son ecuaciones lineales, es decir,  todos los monomios deben ser de grado 1!

Por ejemplo, los siguientes sistemas de ecuaciones no son lineales.

Fijaos en estos casos, como o bien las incógnitas se están multiplicando  o bien están elevadas al cuadrado (monomios de grado dos)  . Este tipo de ecuaciones las aprenderemos a resolver en 4ºESO.


¿QUÉ ES RESOLVER UN SISTEMA?
 Resolver un sistema consiste en determinar los valores de x e y, que hacen de las ecuaciones una identidad, es decir, que hacen que las dos igualdades sean ciertas.

Ejemplo: Es fácil comprobar que las soluciones del sistema

 x + y = 7    

2x + y = 10, 

son x=3, y=4,  ya que    3+4=7   y    2·3+4 = 6 + 4 = 10.

Podéis  pensar cuáles podrían ser las soluciones del sistema:

3x + 2y  = 13,  

x + y =  5.

TAREA 1: Comprueba en los siguientes sistemas, que sus soluciones son los números que se indican debajo:

¿CÓMO RESOLVER UN SISTEMA?

 Los matemáticos interesados en estos temas, han ideado diferentes métodos para resolver sistemas de ecuaciones sin necesidad de ir probando con todos los números imaginables (sería una tarea poco práctica).  Los principales métodos de resolución son.

• Método de sustitución.
• Método de igualación.
• Método de reducción.
• Método gráfico.

Existen muchos otros, pero estos son los clásicos y  más enseñados. Yo hoy os voy a contar sólo el método de sustitución.

    Los pasos que debéis seguir son los siguientes:

1. Escoge una de las ecuaciones, generalmente la más sencilla.
2. Despeja una de las incógnitas, por ejemplo la y.
3. Sustituye la expresión obtenida en la otra ecuación para obtener una ecuación de primer grado sin y (solo con x)
4. Resuelve la ecuación para obtener el valor de x.
5. Finalmente calcula el valor de y, sustituyendo el valor de x obtenido.

     Puedes seguir todos estos pasos,  en el siguiente ejemplo sacado del libro. 

 Ahora te toca a tí...

TAREA: Realiza los ejercicios 1 y 2 de la página 173, para practicar el método explicado.

Estos ejercicios los tenéis disponibles en vuestro libro de Matemáticas 2ºESO.

Como siempre, una vez realizada la tarea en el cuaderno debéis enviarla escaneada a la dirección de correo:   fedematesxxi@gmail.com

  Este correo también lo tenéis disponible para dudas. Gracias por la atención. 

 ------------------------------    FIN   DE  LA   CLASE  --------------------------------

Próxima sesión: Miércoles 25  de Marzo de 2020

Clase 3: Repaso del tema de ecuaciones.

Buenos días!

Espero que estéis todos/as bien,  ahí detrás del ordenador. Tras el descanso de ayer, volvemos nuevamente con una clase de Matemáticas, en la que vamos a repasar los últimos contenidos estudiados.

Quiero deciros, antes de nada, que no hagáis las tareas con prisas ni agobios. Organizad bien vuestro tiempo para que podáis dedicar 10-15 minutos máximo a cada asignatura.  Además todas las clases van a quedar aquí publicadas, y por tanto podéis consultarlas las veces que os sean necesarias.
Como no tenemos prisa, podéis ir haciendo  las tareas a vuestro ritmo y  cuando las tengáis hechas en el cuaderno, las vais enviando, ok?

Dicho esto, nos dirigimos a la pizarra  y comenzamos ....

¿QUÉ TENEMOS QUE SABER DEL TEMA?
En este tema (tema 7 del libro), hemos visto qué es una ecuación  y como resolverla. Más exactamente, hemos aprendido a resolver ecuaciones de primer y segundo grado, porque a partir de ahí todo se vuelve mucho más complicado. Os dejo lo que tenéis que tener claro:

• Distinguir entre ecuación e identidad.
• Resolver ecuaciones de primer grado con paréntesis y denominadores.
• Distinguir entre ecuaciones sin solución (incompatibles), con solución (compatibles) y con infinitas soluciones (identidad)
• Resolver una ecuación de segundo grado completa.
• Plantear y resolver problemas haciendo uso de ecuaciones.

Para repasar todo esto os dejo la tarea de hoy. Tenéis todo el fin de semana para hacerla.

TAREA: Realizar la  autoevaluación, ejercicios del 1 al 8, del tema 7 (página 157) del libro de Matemáticas. 

Estos ejercicios los tenéis disponibles en la página 157 de vuestro libro de Matemáticas 2ºESO.

Como siempre, una vez realizada la tarea en el cuaderno debéis enviarla escaneada a la dirección de correo:   fedematesxxi@gmail.com

  Este correo también lo tenéis disponible para dudas. Gracias por la atención. 

 ------------------------------    FIN   DE  LA   CLASE  --------------------------------

Próxima sesión: Lunes 23 de Marzo de 2020

CLASE 2: Resolución de problemas.

 Buenos días a todos/as!

En la clase de hoy vamos a repasar la resolución de  problemas con  ecuaciones. Recordad que el lenguaje algebraico es un lenguaje nuevo (el lenguaje de las matemáticas) y por tanto al principio cuesta un poco, pero es necesario aprenderlo bien. Es una herramienta útil para resolver muchos problemas, que en principio pueden parecernos  tremendamente complicados.

Nuestra clase de hoy tiene dos partes:

1. Una parte de lectura de la lección en el blog.

2. Una parte de tareas para realizar en el cuaderno y enviar al profesor.

Puesto que todas las  lecciones permanecerán subidas al blog, podéis usar este recurso las veces  que os sea necesaria, para su consulta. 

¿CÓMO RESOLVER UN PROBLEMA  CON ECUACIONES?
Los pasos que debes seguir para resolver un problema de ecuaciones son:

1. Leer detenidamente el problema, tomando los datos necesarios.
2. Determinar qué representa la incógnita (a qué llamamos x)
3. Con los datos del enunciado escribir una ecuación.
4. Resolver la ecuación obtenida.
5. Expresar las soluciones correctamente, comprobando la validez del resultado.

Veamos algunos ejemplos:

PROBLEMA 1:   Si a un número le sumamos su doble y luego su triple obtenemos 60. ¿De qué número se trata?

Solución:  Llamamos x al número desconocido. La ecuación será: x + 2x +3x = 60.

Resolviendo la ecuación  6x= 60,   luego x=10, que es la solución buscada.

PROBLEMA 2:  Un kilo de manzanas cuesta cincuenta céntimos más que uno de naranjas. Si hemos comprado 2 kg de manzana y cuatro de  naranjas, y nos han cobrado 5,80€, determina el precio de un kilo de naranjas.

Solución:  Llamamos x  al precio de un kg de naranjas (que es lo que nos piden). 

                  x: precio del kg de   naranjas 

                  x+0,50:  precio del kg de  manzanas.

  La ecuación pedida es:  2(x+0.50) + 4x = 5,80 

  Resolvemos la ecuación:    2x + 1 + 4x = 5,80 

                                              2x + 4x = 4.80

                                                 6x = 4.80 

                                                    x= 0,80 €

         

                        Luego el kilo de naranjas está a 80 céntimos. 

TAREAS (Para resolver en el cuaderno)

Realizar los problemas del 14 al 17,  y los problemas 25 y 26  de la página 152 del libro de Matemáticas.

 Una vez realizados (copiando enunciados) deben enviarse al siguiente correo electrónico para su corrección:  fedematesxxi@gmail.com

No olvidéis que también disponéis del correo o este blog para plantear dudas.

CLASE 1: Resolviendo ecuaciones de 2º grado.

Buenos días a todos/as!

Espero que estéis   siguiendo las clases de Matemáticas desde casa. Este blog se va a convertir estos días en nuestra pizarra, e iremos dando todos los días  alguna lección para ir avanzando en el temario. También al final de la explicación os propondré tarea.

Todo lo que os vaya contando aquí, podéis pasarlo a vuestro cuaderno, (en bolígrafo azul y buena letra) o al menos lo más importante, para que os queden claras las explicaciones. Si hay alguna duda podéis enviar vuestros comentarios al final de la entrada (del blog) o a través del correo electrónico:

fedematesxxi@gmail.com

REPASANDO ECUACIONES DE 2º GRADO

TAREA 1:  Las tareas que proponemos debéis pasarlas al cuaderno, copiando enunciados  y realizándolas a lápiz. Una vez hechas todas las tareas del día, debéis enviarlas por correo para su corrección. La mayoría están sacadas del libro de Matemáticas. Como la siguiente:

   Ayuda: Primero debéis quitar los  paréntesis, y luego pasar ordenadamente todos los factores al primer miembro, para obtener una expresión igualada a cero.


LA ECUACIÓN DE SEGUNDO GRADO COMPLETA (Fórmula general)

         Aunque no aparece bien en la imagen, la raíz cuadrada abarca a todo el  término b^2 - 4ac.
         Esto  es lo que se conoce como discriminante de la ecuación. Mirad como se resuelven:

    

TAREA 2:  Realiza en tu cuaderno los siguientes ejercicios sobre ecuaciones de segundo grado, indicando el valor del discriminante y el número de soluciones obtenidas. ¿Qué observas?

• Una vez realizadas las tareas 1 y 2  en el cuaderno,  debéis pasarlas a un documento en word o libreoffice,  (o bien haciendo una foto al trabajo hecho) , y lo enviáis por correo para su calificación.

TAREAS DIGITALES (en Educa3d.com)
Si habéis entendido esta parte, vamos a hacer algo más entretenido.
Vais a pinchar en el siguiente enlace:
https://www.educa3d.com/joomla/matematicas-2-eso-ejercicios-resueltos-interactivos#ecuaciones-segundo-grado

Si lo hacéis bien os llevará a la siguiente página:

Es un portal donde tenéis disponibles muchas presentaciones y unidades interactivas de matemáticas.  Vamos a practicar las ecuaciones de un modo interactivo.
 Seguid las siguientes instrucciones: 

• Leed bien que ponga Ecuaciones segundo grado (básico).
• Pinchad donde pone "miniunidad interactiva",  Os aparecerá una nueva pantalla, y dadle a "continuar."
• Te preguntarán si puedes ver la animación. Dile que SI  y sigue.
• Se debe abrir una nueva pantalla, como ésta:

• Pincha donde pone "Alum@".
• Introducid nombre y dirección de correo. O bien dadle a continuar. 
• Aparecerá la opción de evaluar o por libre. Escoged primero la opción "libre". 
• Os aparecerá una nueva página, con teoría y ejercicios para practicar esta parte.

• Seleccionad primero la teoría para ver toda la explicación en cada apartado.
• Tras visualizar la teoría realizad on-line, los ejercicios interactivos propuestos. Es entretenido y os servirá para aprender esta parte del  tema.
• Disponéis de 5 intentos para cada tarea, antes de pasar a la siguiente.
• Una vez finalizada pasad a modo evaluación, para autoevaluaros vosotros mismos.

            __________________            FIN DE LA CLASE        __________________


          Contenidos de la próxima sesión:  Resolución de problemas de ecuaciones.

SUSPENSIÓN DE CLASES EN CENTROS EDUCATIVOS

Como ya sabréis, estamos en un período excepcional de alarma sanitaria, por la expansión del virus COVID-19. La Consellería de Educación de la Comunidad de Valencia, ha decidido suspender todas las clases presenciales, en todos los niveles educativos, a partir del próximo Lunes 16 de Marzo, y con carácter indefinido. Esto significa que no sabemos cuando volveremos a dar clase con total normalidad.

Por esta razón, y para no perder el ritmo del curso, estamos pensando en pasar a un modo de formación on-line, donde el seguimiento se haga a través de los canales que nos ofrecen las nuevas tecnologías (plataforma ITACA, cursos en internet, tablets, móviles...)

De momento comenzaremos haciendo uso de nuestro blog, que lleva funcionando desde principio de curso. Diariamente os iré subiendo contenidos y material para que lo vayáis trabajando en casa. El procedimiento es muy simple.

• Elaborad un horario de estudio en casa para cada día  con ayuda de vuestros padres.Usad el horario de clase, como referencia. 
• En ese horario semanal, tendréis que establecer un tiempo para estudiar cada una de las asignaturas del curso: Lengua, Inglés, Matemáticas, Ciencias Naturales, .etc... un poco de tiempo diario para cada una de ellas es suficiente. 
• En nuestra asignatura de Matemáticas,  os propondremos lo que tenéis que leer del libro y las actividades a realizar.
• Debéis consultar diariamente este blog, con el fin de ver las tareas propuestas y  seguir con vuestra formación Matemática.

Más adelante estudiaremos la posibilidad de que todos podáis acceder a una plataforma on-line, con el fin de que cada uno vaya subiendo las actividades propuestas para su evaluación.  De momento id mirando las fechas de todas las entradas del blog.
Aquél que tenga cuenta de correo gmail puede comentar online y formular dudas o sugerencias. Sed siempre educados y respetuosos en vuestros comentarios. El que no tenga cuenta, se puede crear una. Es bien sencillo y podréis recibir toda la información que se vaya publicando. Os resultará útil.

Esperemos que  esta situación se normalice cuanto antes y volvamos a vernos en clase pronto.
Un saludo a todos/as.

El profesor

Federico Ruiz L.

Tareas para casa

Aquí tenéis las tareas que debéis realizar para el próximo día:

Fecha:  Lunes 16   de Marzo,  2020
Grupo: 2º ESO - AB
Hora: De 9:30h a 10:00h (según horario establecido)
Aula:  Trabajo en casa.

• Realizar el ejercicio 11 de la página 152 en el cuaderno,  sobre ecuaciones de segundo grado.
• Realizar los problemas del 18 al 24 de dicha página, para practicar la resolución de problemas con ecuaciones.

• Si disponéis de ordenador en casa, podéis realizar los ejercicios usando un procesador de texto (libreoffice o word) y guardarlo como tarea. Podéis enviar dichos ejercicios al correo detallado más abajo para su corrección. Se tendrá en cuenta para la evaluación de los contenidos  y os sirve para trabajar la competencia digital.  

               Hemos dispuesto un correo para resolver las dudas que os vayan surgiendo:                                                                                  fedematesxxi@gmail.com

• IMPORTANTE:  Recordad que el examen trimestral de Marzo se iba a realizar el próximo Miércoles 18 de Marzo, a las 13:00h en el aula P2.  Se suspende la realización del examen hasta nuevo aviso.