CLASE 32: Cuerpos geométricos. Poliedros regulares.

Buenos días!

Espero estéis todos bien en casa. Vamos  a  continuar un día más con nuestras clases de Matemáticas on-blog.  Si recordáis, estábamos estudiando cuerpos geométricos. Y hoy les toca a una clase muy particular de figuras, que por tener, tienen hasta nombre propio. Son los poliedros regulares o sólidos platónicos.

El nombre les viene de un filósofo griego denominado Platón,  que vivió en el siglo IV a.C, y que daba clases en una academia en Atenas.  Realmente el nombre de Platón era Aristocles, pero como era pequeño y de espaldas anchas, su profesor de gimnasia le puso el mote de Platón, que significa precisamente eso, "el de espaldas anchas". Tanto le agradó el apodo, que lo adoptó para el resto de su vida. Se hizo famoso porque colgó  un rótulo a la entrada de su academia, en la que decía: 

                                             "Nadie entre aquí que no sepa geometría!"

Y es que para los griegos, la geometría era sinónimo de educación e inteligencia,  a la que dedicaban  interminables horas de estudio. Nosotros vamos a conocer algo mejor estos sólidos platónicos,  y algunas de sus propiedades.

Abrid vuestro libro de Matemáticas por la página 221,  y seguir la explicación con atención. Hoy es más teoría que práctica...

POLIEDROS REGULARES.

Solamente existen cinco poliedros regulares, y sus caras son o bien todas triángulos equiláteros, o bien todas cuadrados o bien todas pentágonos regulares. Es decir, no existe ningún poliedro regular cuyas caras sean hexágonos, octógonos o figuras de mas lados.  

Los cinco poliedros regulares son:

• Tetraedro: tiene 4  caras, y todas son triángulos equiláteros.
• Hexaedro: o cubo, tiene 6 caras, todas cuadradas (es la forma de un dado)
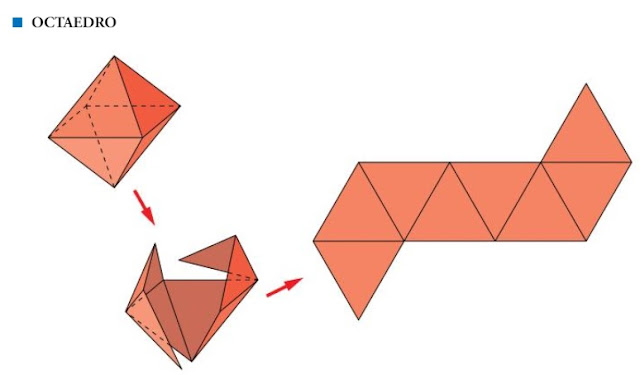
• Octaedro: tiene 8 caras, formadas por triángulos equiláteros.
• Dodecaedro: tiene 12 caras iguales, formadas por pentágonos regulares.
• Icosaedro. tiene 20 caras iguales, y todas son triángulos equiláteros.

DESARROLLOS DE LOS POLIEDROS REGULARES

Todas estas figuras se pueden construir con cartulina a partir de su desarrollo plano. Observa cómo se obtienen en cada caso.

En definitiva, aquí tienes las plantillas con los que poder construirlos.

Para calcular el área total de un poliedro regular, basta calcular el área de una cara y multiplicar por el número de caras.  Copia el siguiente ejemplo en tu cuaderno, como guia:

Ejemplo 1: Calcula el área total de un tetraedro de 12 cm de arista.

Solución:  En primer lugar debemos calcular el área de una cara que es un triángulo equilátero de 12 cm de arista.  Llamando "a", a la altura del triángulo, podemos calcularla  usando el Teorema de Pitágoras. Fíjate en la imagen:

Una vez calculada el área de una cara, la superficie total del tetraedro será 4 veces dicho valor, porque tiene cuatro caras iguales. En definitiva,

                                  Área total  = 4 · 62,4 = 249,6 metros cuadrados.

Si has comprendido hasta aquí vamos a por la primera tarea del día

TAREA 1: Realiza en tu cuaderno los ejercicios 2 y 3 de la página 223,  para el cálculo del área total de poliedros.

La última tarea de hoy es diferente. Se trata de una manualidad, consistente en construir los cinco sólidos platónicos. Para ello necesitarás, cartulina, tijeras, pegamento y mucha paciencia.

En primer lugar necesitarás dibujar los desarrollos planos de cada una de las figuras sobre la cartulina, según las medidas indicadas. Ésto no es fácil y te puedes ayudar de alguna plantilla que esté ya elaborada por internet (hay muchas páginas donde te las puedes descargar gratuitamente e imprimirlas directamente) Luego tendrás que recortarlas y pegarlas, hasta obtener el poliedro regular correspondiente. 

TAREA 2: (Manualidad)  A partir de sus desarrollos planos, construye los cinco poliedros regulares con cartulina, de acuerdo con las siguientes medidas:

• Tetraedro:  10 cm de arista.
• Cubo: 8 cm de arista.
• Octaedro: 6 cm de arista.
• Dodecaedro: 5 cm de arista.
• Icosaedro. 3 cm de arista.

Una vez tengas la construcción hecha de cada figura,  deberás  enviar una foto por separado con el nombre de cada poliedro para su valoración.

De momento es todo por hoy. Espero que os divirtáis con las construcciones. En la próxima lección hablaremos de los cuerpos de revolución. Ya sabéis, aprovechad el tiempo y estudiad mucho!

Como siempre, una vez realizada la tarea en el cuaderno debéis enviarla escaneada a la dirección de correo:   fedematesxxi@gmail.com

  Este correo también lo tenéis disponible para dudas.

--------------------------    FIN   DE  LA   CLASE  --------------------------------

Próxima sesión: Viernes 5  de Junio de 2020.