Hoy lunes, vamos a comenzar un tema nuevo, pero que es continuación del tema de ecuaciones. Se trata del tema 8 del libro y tiene por título "Sistemas de ecuaciones". Ya sabéis que debéis ir elaborando vuestros apuntes en el cuaderno de Matemáticas, copiando algunas de las explicaciones y luego realizando las tareas propuestas. Así que prestad atención a la pizarra porque comenzamos...
En este tema (tema 8 del libro), vamos a ver un tipo de ecuaciones muy particular.
Un sistema de ecuaciones lineales es un conjunto de ecuaciones con varias incógnitas. Como esto puede ser muy complicado, nosotros sólo vamos a aprender a reconocer y resolver sistemas de dos ecuaciones con dos incógnitas, aunque ya os adelanto que hay sistemas de tres ecuaciones con tres incógnitas e incluso de veinte ecuaciones con veinte incógnitas (eso se lo dejamos a los de Bachillerato)
Lo que vamos aprender:
- Reconocer un sistema de ecuaciones lineales.
- Resolver sistemas de ecuaciones por el método de sustitución.
- Resolver sistemas de ecuaciones por el método de reducción.
- Resolver problemas de ecuaciones con algunos de los métodos estudiados.
- Resolver sistemas de ecuaciones por el método gráfico.
¿QUÉ ES UN SISTEMA DE ECUACIONES LINEALES?
Un sistema de dos ecuaciones lineales con dos incógnitas (x,y), es un conjunto formado por dos ecuaciones del tipo: ax + by =c.
Ejemplos: Son sistemas de este tipo:
Fijaos la forma que tienen. Sólo aparece la x y la y, acompañado de unos coeficientes e igualado a un número. Cuando algunas de las incógnitas aparece elevada a dos, o tres ya no son ecuaciones lineales, es decir, todos los monomios deben ser de grado 1!
Por ejemplo, los siguientes sistemas de ecuaciones no son lineales.
Fijaos en estos casos, como o bien las incógnitas se están multiplicando o bien están elevadas al cuadrado (monomios de grado dos) . Este tipo de ecuaciones las aprenderemos a resolver en 4ºESO.
¿QUÉ ES RESOLVER UN SISTEMA?
Resolver un sistema consiste en determinar los valores de x e y, que hacen de las ecuaciones una identidad, es decir, que hacen que las dos igualdades sean ciertas.
Ejemplo: Es fácil comprobar que las soluciones del sistema
son x=3, y=4, ya que 3+4=7 y 2·3+4 = 6 + 4 = 10.
Podéis pensar cuáles podrían ser las soluciones del sistema:
TAREA 1: Comprueba en los siguientes sistemas, que sus soluciones son los números que se indican debajo:
¿CÓMO RESOLVER UN SISTEMA?
Ahora te toca a tí...
TAREA: Realiza los ejercicios 1 y 2 de la página 173, para practicar el método explicado.
Un sistema de dos ecuaciones lineales con dos incógnitas (x,y), es un conjunto formado por dos ecuaciones del tipo: ax + by =c.
Ejemplos: Son sistemas de este tipo:
Por ejemplo, los siguientes sistemas de ecuaciones no son lineales.
¿QUÉ ES RESOLVER UN SISTEMA?
Resolver un sistema consiste en determinar los valores de x e y, que hacen de las ecuaciones una identidad, es decir, que hacen que las dos igualdades sean ciertas.
Ejemplo: Es fácil comprobar que las soluciones del sistema
x + y = 7
2x + y = 10,
Podéis pensar cuáles podrían ser las soluciones del sistema:
3x + 2y = 13,
x + y = 5.
TAREA 1: Comprueba en los siguientes sistemas, que sus soluciones son los números que se indican debajo:
¿CÓMO RESOLVER UN SISTEMA?
Los matemáticos interesados en estos temas, han ideado diferentes métodos para resolver sistemas de ecuaciones sin necesidad de ir probando con todos los números imaginables (sería una tarea poco práctica). Los principales métodos de resolución son.
- Método de sustitución.
- Método de igualación.
- Método de reducción.
- Método gráfico.
Existen muchos otros, pero estos son los clásicos y más enseñados. Yo hoy os voy a contar sólo el método de sustitución.
Los pasos que debéis seguir son los siguientes:
- Escoge una de las ecuaciones, generalmente la más sencilla.
- Despeja una de las incógnitas, por ejemplo la y.
- Sustituye la expresión obtenida en la otra ecuación para obtener una ecuación de primer grado sin y (solo con x)
- Resuelve la ecuación para obtener el valor de x.
- Finalmente calcula el valor de y, sustituyendo el valor de x obtenido.
Puedes seguir todos estos pasos, en el siguiente ejemplo sacado del libro.
Ahora te toca a tí...
TAREA: Realiza los ejercicios 1 y 2 de la página 173, para practicar el método explicado.
Estos ejercicios los tenéis disponibles en vuestro libro de Matemáticas 2ºESO.
Como siempre, una vez realizada la tarea en el cuaderno debéis enviarla escaneada a la dirección de correo: fedematesxxi@gmail.com
Este correo también lo tenéis disponible para dudas. Gracias por la atención.
------------------------------ FIN DE LA CLASE --------------------------------
Próxima sesión: Miércoles 25 de Marzo de 2020
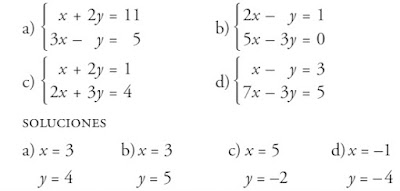
No hay comentarios:
Publicar un comentario