Buenos días!
Comienza una nueva semana, y continuamos con nuestras lecciones de Matemáticas on-blog. Os recuerdo que estaremos subiendo lecciones hasta el miércoles 10 de Junio, fecha en la que podemos considerar finalizado el período lectivo de este curso 2019/20. El objetivo de estos días es terminar de impartir los contenidos relacionados con la geometría, y más precisamente, con el área y volúmenes de cuerpos geométricos. El resto de días, serán de repaso.
La clase de hoy la vamos a dedicar a las pirámides. Así que coged vuestro libro de Matemáticas, abridlo por la página 218, el cuaderno por donde corresponda, bien dispuestos en el escritorio, y cuando estéis preparados comenzamos...
PIRÁMIDES
A todo el mundo le suena la palabra pirámide, que suele asociar con las famosas pirámides de Egipto. Pero lo que no todo el mundo sabe, es que la palabra pirámide viene del griego "pyros" que significa "fuego". Y es que la forma de una pirámide se parece a la del fuego, ancha en la base y estrecha en su parte superior, También famosas son las piras funerarias, que desde antiguo, servían para incinerar los cuerpos de los fallecidos, en una especie de ritual sagrado.
Desde un punto de vista matemático, una pirámide es la forma que adopta un poliedro que sólo tiene una base y un vértice. Sus caras laterales son triangulares.
Copia en tu cuaderno:
CLASIFICACIÓN DE LAS PIRÁMIDES.
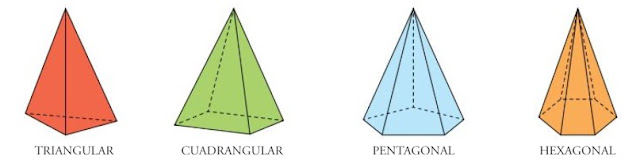
Las pirámides, al igual que los prismas, se clasifican en función del polígono de la base. Así hablamos de pirámides triangulares, cuadrangulares, pentagonales, hexagonales....
DESARROLLO PLANO DE UNA PIRÁMIDE
Es decir, en el desarrollo plano de una pirámide obtenemos una base, que es un polígono (regular o irregular), y una serie de caras laterales triangulares, tantas como lados tenga la base. Esto nos da una idea de como calcular el área total de la figura.
SUPERFICIE DE UNA PIRÁMIDE
Fijaos bien y no confundid la apotema de la base (a) con la apotema de la pirámide (a'). La primera la necesitamos para calcular el área de la base. La segunda para calcular el área lateral de la figura, y se encuentra sobre una cara lateral. El área total será la suma de ambas, como aparece en la fórmula indicada más arriba.
Veamos un par de ejemplos, para que quede todo más claro.
Ejemplo 1:
Ejemplo 2:
Fijaos en el segundo ejemplo como mientras que la apotema de la base mide 5,2 cm (la raíz cuadrada de 27), la apotema de la pirámide mide 14 cm y en ambos casos se han determinado a través del Teorema de Pitágoras. De hecho, hemos necesitado calcular primero la apotema de la base, para calcular la apotema de la pirámide. Así que aquí el orden en que se calcula cada cantidad es importante..
Vamos a practicar esta parte con la primera tarea del día.
TAREA 1: Realiza en tu cuaderno los ejercicios 1 y 2 de la página 219, sobre pirámides.
(Una vez realizada la tarea, continuamos...)
VOLUMEN DE LA PIRÁMIDE
Es decir, el volumen de la pirámide es igual al área de la base por su altura entre tres, o lo que es lo mismo, a igualdad de altura y base, una pirámide posee la tercera parte del volumen del prisma.
Ejemplo 3
TAREA 2: Realiza en tu cuaderno los ejercicios 1 y 2 de la página 246, para el cálculo del volumen de pirámides.
NOTA: En este último ejercicio, debes explicar razonadamente todas los pasos, indicando primero el área de la base, y luego el volumen total de la figura.
De momento es todo por hoy. En la próxima lección explicaremos algo sobre poliedros regulares. Aprovechad el tiempo y estudiad mucho!
Como siempre, una vez realizada la tarea en el cuaderno debéis enviarla escaneada a la dirección de correo: fedematesxxi@gmail.com
Este correo también lo tenéis disponible para dudas.
-------------------------- FIN DE LA CLASE --------------------------------
Próxima sesión: Miércoles 3 de Junio de 2020.
No hay comentarios:
Publicar un comentario